神经网络是一种机器学习程序或模型,它以类似于人脑的方式做出决策,通过使用模仿生物神经元协同工作方式的过程来识别现象、权衡利弊并得出结论。
0. 先了解几个公式
L2范式
$$ \|W\|_2=\sqrt{w_1^2+w_2^2+w_3^2+w_4^2+\cdots} $$
Sigmod函数
$$ sigmod(x) = \frac{1}{1+e^{-x}} $$

softmax
$$ \begin{aligned} & \operatorname{softmax}(\hat{Y}) =\frac{e^{\hat{y}_i}}{\sum_{j=1}^4 e^{\hat{y}_j}} \end{aligned} $$
1. 神经网络模型
最左边一层为输入层,对应数据的维度,数据通过这一层输入到神经网络。

神经网络中任意一个神经元 都会和上一层、下一层所有的节点相连,所以也叫做全连接神经网络。
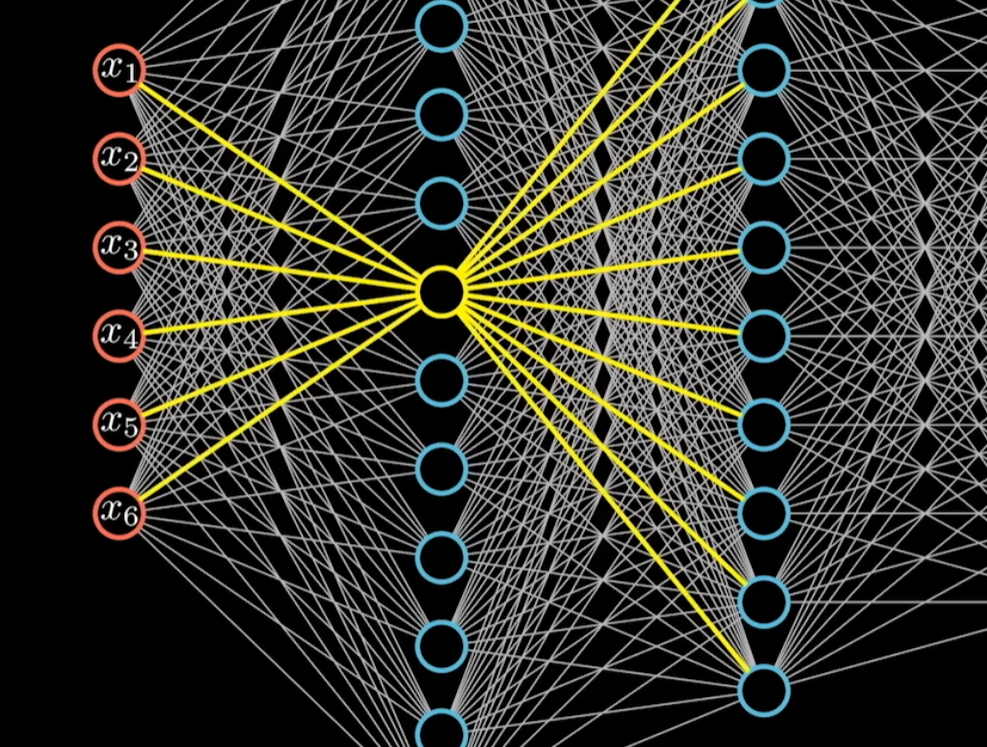
每一条边代表权重系数。

表示一个线性方程。
$$ w_1 x_1+w_2 x_2+w_3 x_3+w_4 x_4+w_5 x_5+w_6 x_6+b=z $$
结果z还要进行一个函数运算才会输出到下一层,,该函数叫激活函数,sigmoid是符合激活函数要求的函数之一。(应该得是一个非线性函数

激活的过程直接使用神经元来表示。
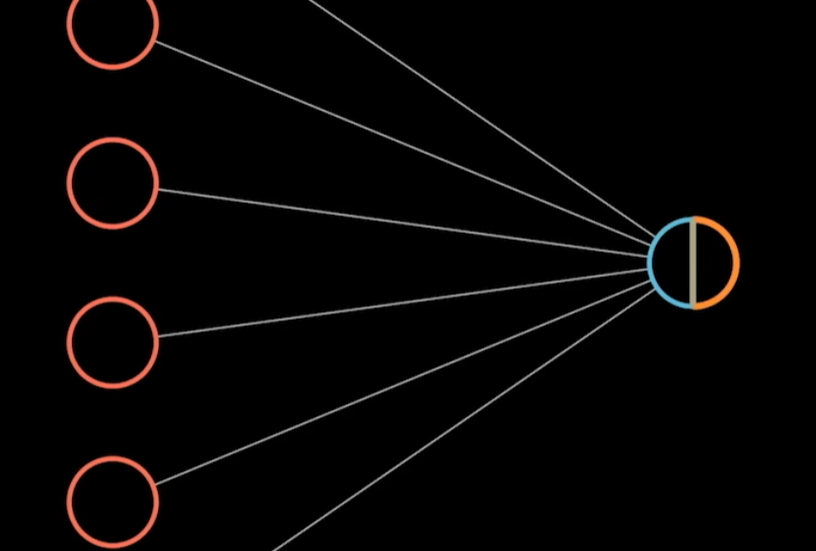
以一个二维数据为例。
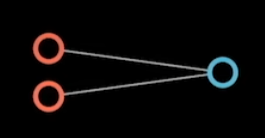
公式为
$$ \left[\begin{array}{l} x_1 \\ x_2 \end{array}\right]^T \cdot\left[\begin{array}{l} w_1 \\ w_2 \end{array}\right]+[b]=[z] $$
$$ \operatorname{sigmoid}(z)=a $$
图像为
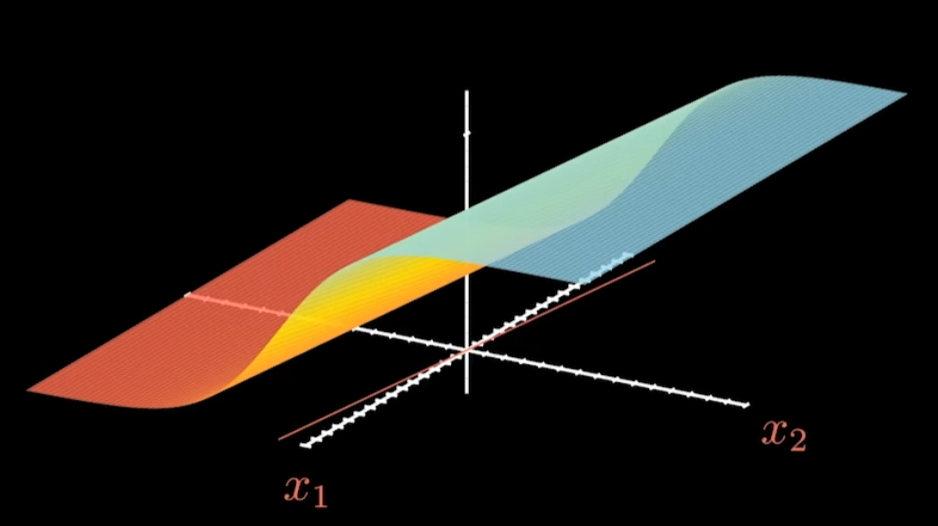
增加一层神经元。
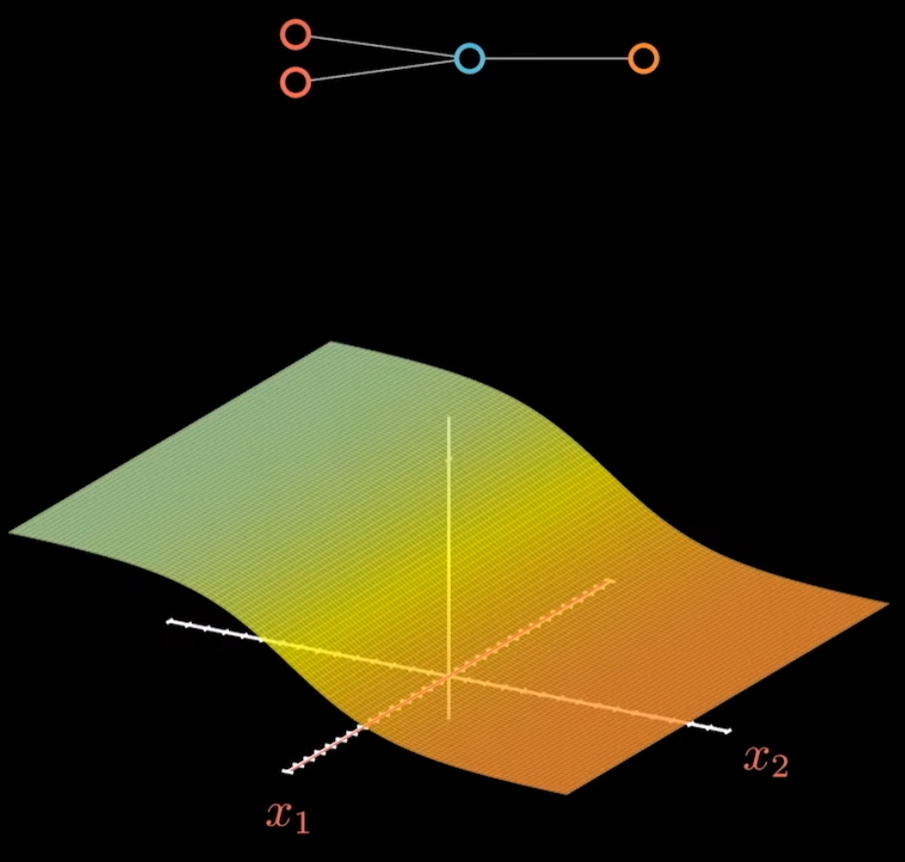

第一层增加一个神经元。
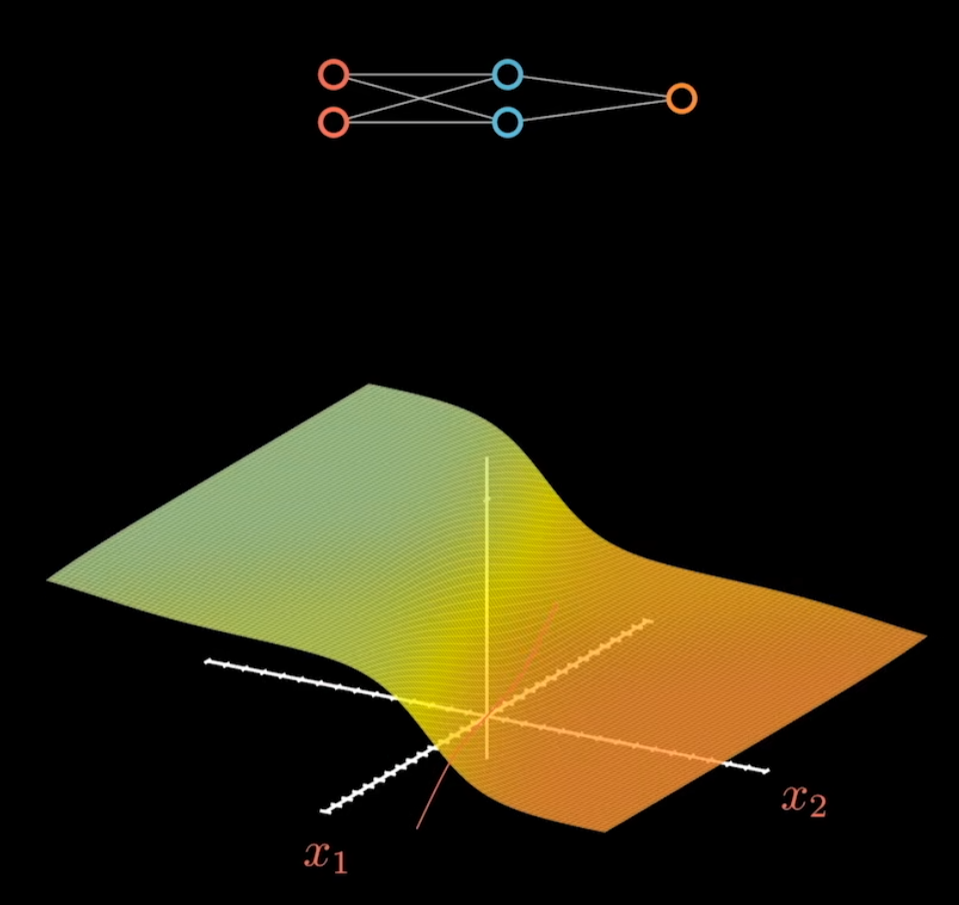

增加到四个神经元。


继续增加神经元。
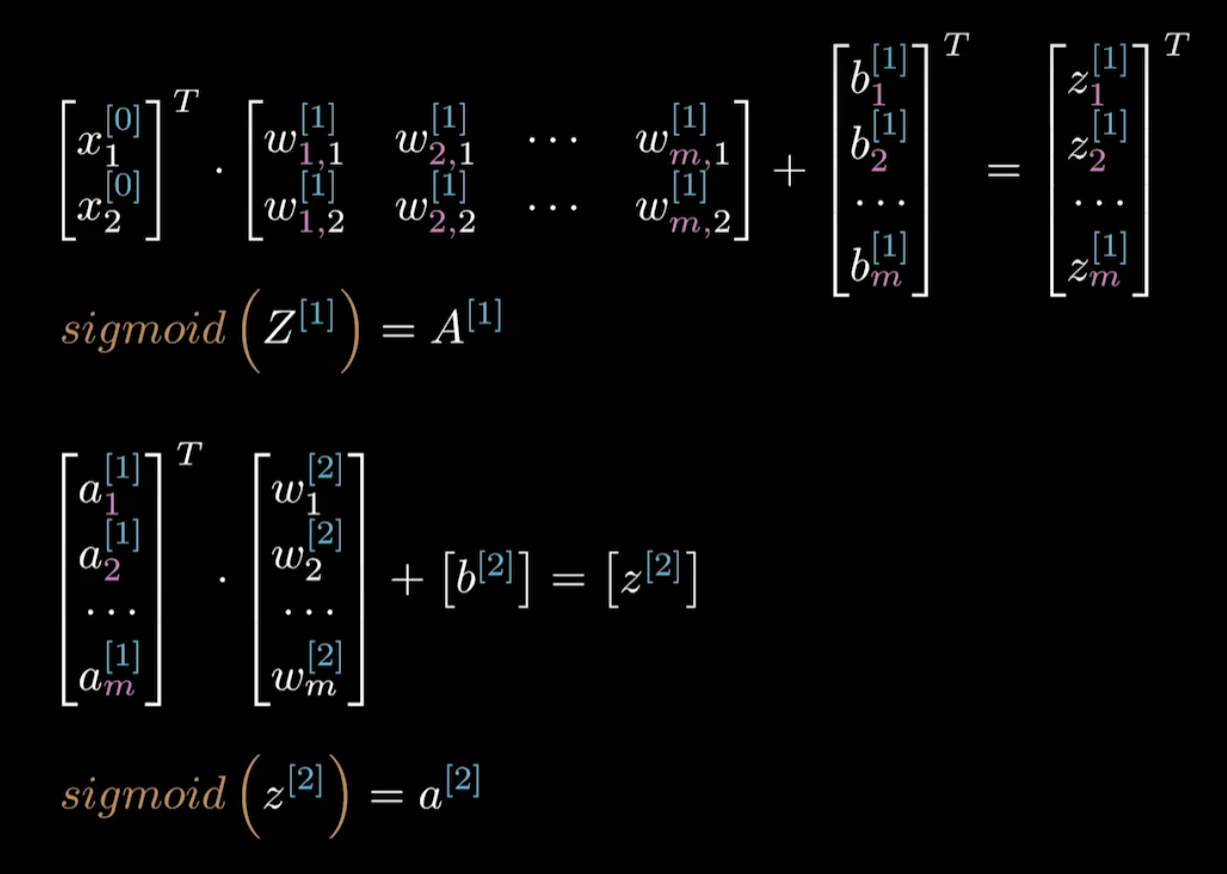



图像的复杂程度会越来越高,只要神经元足够多,任何一种复杂的平面都可以被无限接近的表达出来,这个叫做万能逼近定理,或者通用近似定理。
2. 激活函数
实现万能逼近的关键之一就是激活函数。
其他常用的激活函数:
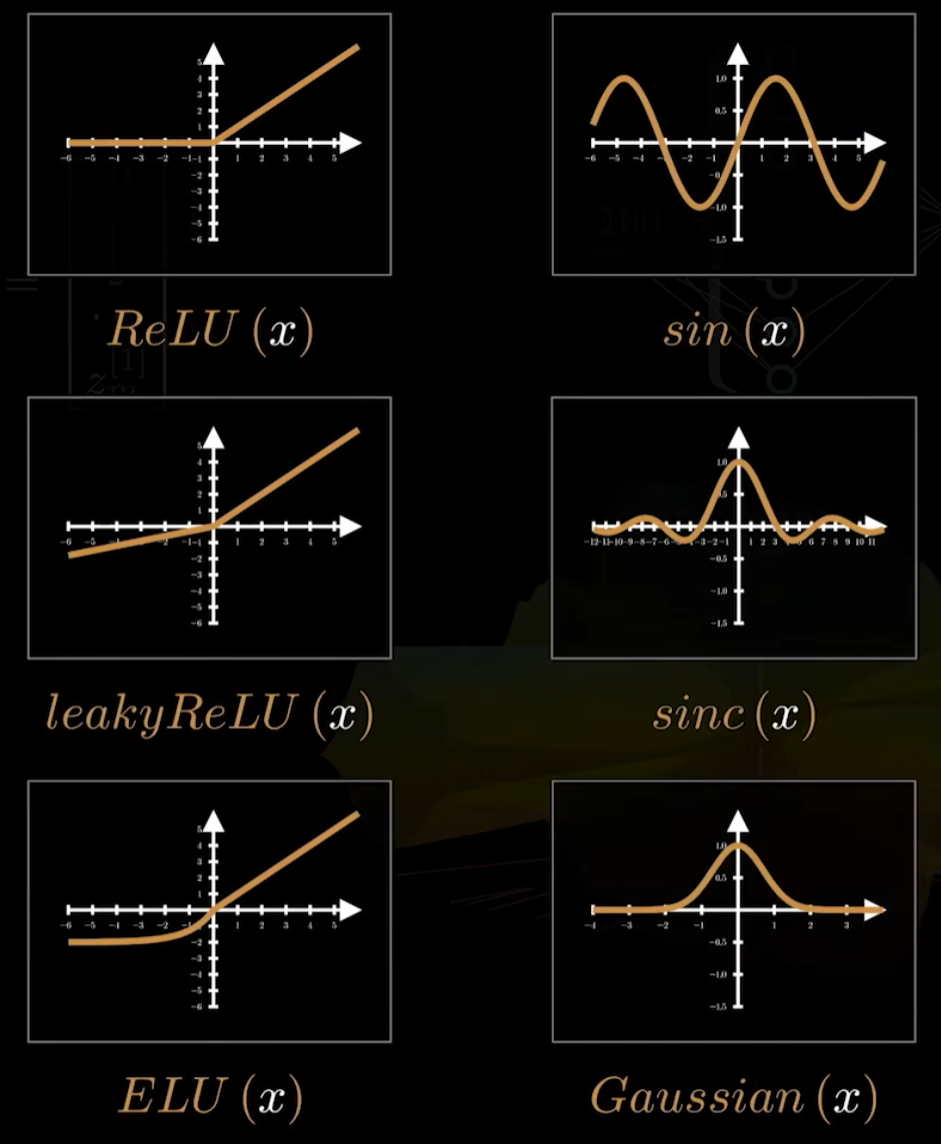
神经网络的复杂性来自于激活函数。
3. 回到神经网络
假如数据都分布在二维平面,掺杂在一起很难直接用直线进行划分。

对数据升维后就可以用更简单的模型将他们分开。

因此可以将中间这一层看做是对数据的升维操作,维度足够多就一定可以找到一个超平面,完成对数据的划分。

神经网络可以有多个输出节点,来处理多分类问题。

Sigmoid函数,蓝色代表一种情况,橙色代表另一种,实现归一化。

多分类中,softmax也这样理解,也可以看作是归一的。
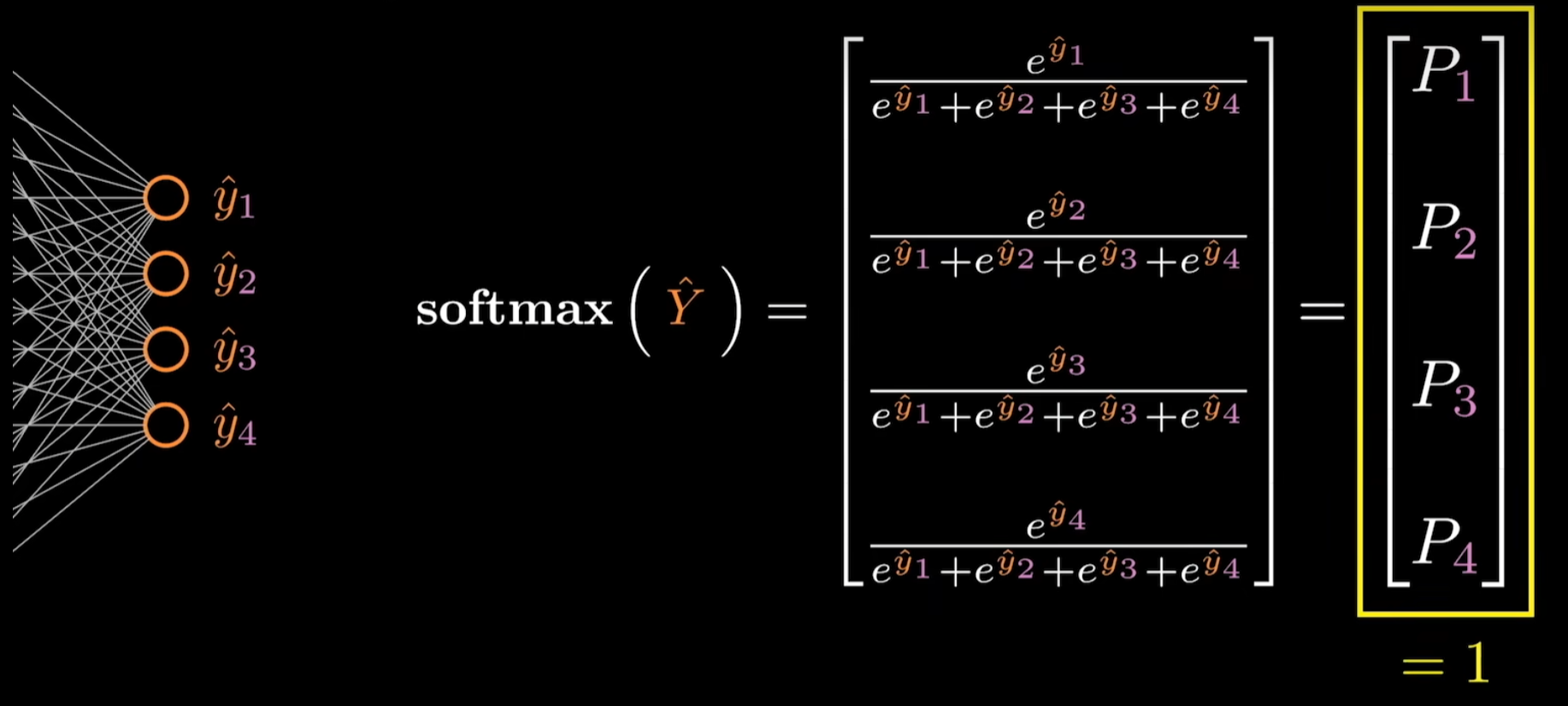
看起来softmax就是sigmoid函数的升级版。
结构是这样的。

隐藏层可以让模型更复杂。
隐藏层可以是进行升维,也可以是进行降维,视频里讲的挺细的,可以去看视频,大概从29分钟开始。
隐藏层越深,抽象程度越高。
机器学习三要素:模型、策略、算法
隐藏层搞定模型,输出层搞定策略,下面来说算法!
算法就是反向传播,关键是梯度下降法。
梯度下降
梯度下降法中,这个 η 指梯度下降的步长,也叫学习率,这是一个超参数,即由我们手动设置而不是由神经网络得到。
步长过短导致较慢达到极值,步长过长导致反复横跳无法收敛。

梯度的另一个表示方法:$ \nabla f $ 读作 奶不乐 艾弗
在求解梯度的时候,把整个神经网络看作是一个黑盒子,里面就是这些表达式。

可以这样表达其中的分量,下标i、j、k分别表示不同的神经元。
$$ \begin{aligned} & \operatorname{ReLU}\left(X \cdot W^{[1]}\right)=A^{[1]} \\ & f_k^{[1]}\left(w_k^{[1]}\right)=a_k^{[1]} \\ & \operatorname{ReLU}\left(A^{[1]} \cdot W^{[2]}\right)=A^{[2]} \\ & f_j^{[2]}\left(A^{[1]}, w_j^{[2]}\right)=a_j^{[2]} \\ & \operatorname{softmax}\left(A^{[2]} \cdot W^{[3]}\right) \\ & f_i^{[3]}\left(A^{[2]}, w_i^{[3]}\right)=a_i^{[3]} \end{aligned} $$
这一块后面没听懂,后面再看一个梯度下降的相关视频吧。
感谢!
工匠总是会在建筑完成后把脚手架拆除。 ——约翰·卡尔·弗里德里希·高斯
高斯就像是一只狡狚的狐狸,总是用尾巴抹去地上的痕迹。 ——尼尔斯·阿贝尔
“原来是这样!”