1 编码&解码
什么是“码”:剥离掉语言中符号等等发音等等形式的不同后,剩下来的单纯的语义关系。
编解码两个步骤:
- 语义关系数字化
- 能正确表示token之间的距离
两种方法:
- 分词器 tokenizer:所有token表示为一维的一个数字
- 独热编码 one-hot:所有token表示为一个维度,且模长为1,分布在一个高维球面上
问题:
- 分词器不能正确表现语义关系,毕竟一维层面,也不能正确表现组合语义,比如两个词语相加后的数值已经被另一个词语所占用
- 独热编码维度又太高,信息密度稀疏,token之间的联系仅体现在维度层面,没有利用空间长度
解决:
- 基于分词后ID升维
- 基于one-hot降维
降维,矩阵计算
2 矩阵和空间变换基础
要理解 向量 乘 矩阵 的本质。
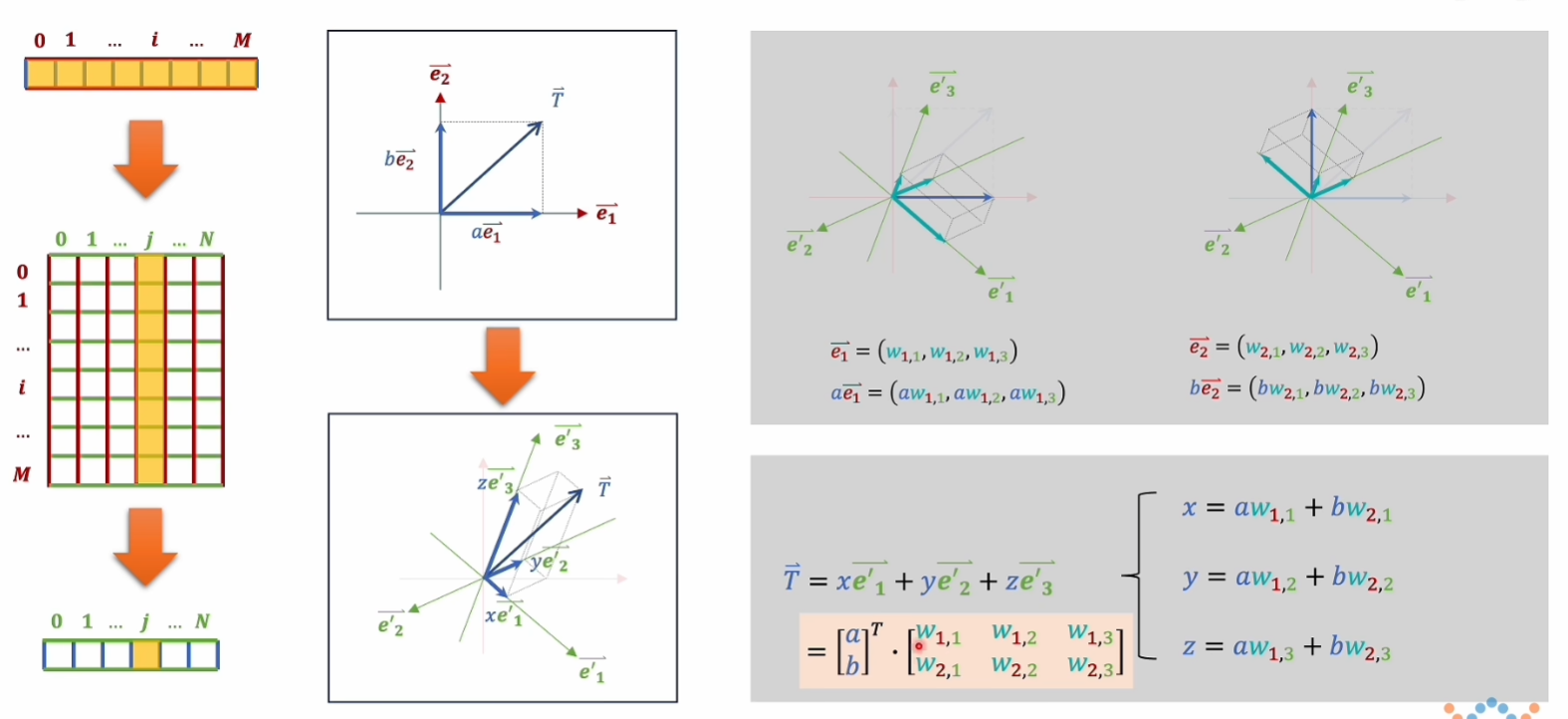
向量是原M维坐标系中各个坐标轴的数值,矩阵是原坐标系中M个坐标轴,每个坐标轴的单位向量在新N维坐标系中每个坐标轴的分量,进行乘法后得到的是原来的向量在新N维坐标系中各个坐标轴的数值,即 M维数值 $ \times $ M在N上单位向量分量 = N维数值
发现:
左下矩阵的行数,即为旧坐标系,也就是乘法中前面的向量所在空间的维度;
左下矩阵的列数,即为新坐标轴,也就是乘法中后面的矩阵所在空间的维度。
乘法的结果就是向量T在新坐标轴中的坐标表示。
矩阵乘法为线性变化,原坐标系的一个点唯一对应新坐标系的一个点,即只能做的旋转或直线上的拉伸和收缩。
二次型可以实现把旧坐标系的直线变成新坐标系的不是直线。
矩阵乘法,原空间两个向量平行、共线,新空间依旧平行、共线,绝对长度可能发生变化,但是比值不会变。
前面讲的向量乘矩阵,那么矩阵A乘矩阵b,矩阵A就可以理解为多个向量,空间变化的规则由B决定。
3 神经网络基础
【多模态学习】神经网络 - 御坂领域 (misakastone.com)
4 词嵌入
【多模态学习】词嵌入 - 御坂领域 (misakastone.com)
潜空间:没有符号、发音等形式上差别的、纯粹的语义空间。
利用潜空间进行中英文翻译,easier!
编解码:赛博版曹冲称象(利用潜空间)
编解码的出现意味着,人工智能所能做的事情已经超越了约翰塞尔所提出的中文房间实验理论,他认为AI无法理解语义。
我们可以这样理解,一个TKOKEN被嵌入之后,每个维度代表一个语义,就可以体现分词器所体现不了的复杂语义关系。

实际的算法中每个维度的意义,我们根本看不懂。
5 Word2Vec
大多的机器学习模型的训练目标是为了完成某个任务,而Word2Vec模型的目标是嵌入矩阵,即:目标不是模型的结果,而是模型的参数(完成任务的方法)。
5.1 CBOW
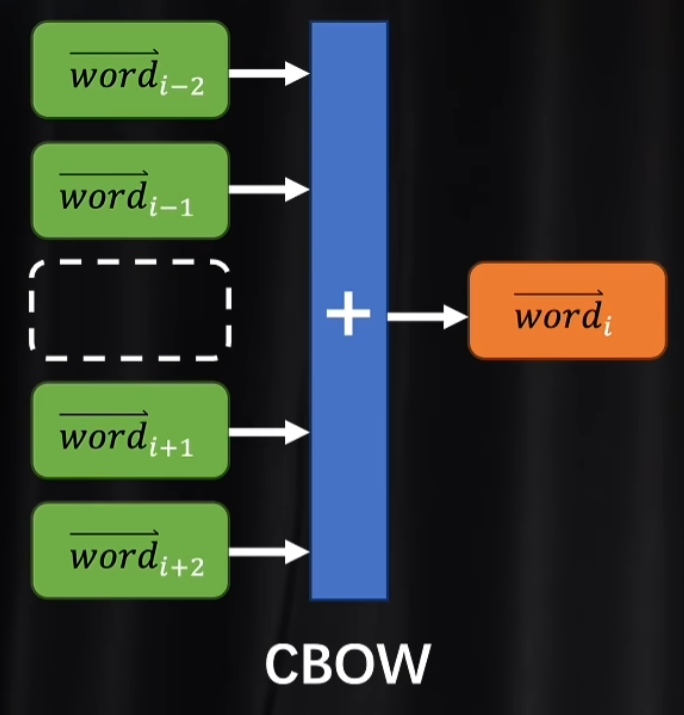
准备奇数个TOKEN,取出第i个,剩下的偶数个TOKEN分别与同一个嵌入矩阵相乘,就得到了潜空间里的词向量,再把这些词向量合成为一个,再解码,让损失函数定量的去看这个和向量解码后和TOKEN i是不是一样的,如果不一样就修改参数。
为什么可以用这个和向量和TOKEN i做比较,因为一个词的语义可以由上下文所推断出来。
反例:这是一个__苹果。
空的词语中可以填“甜” “红” “便宜”,即使不能正确推断,但这也有可能是因为训练数据不够大,上下文信息不够多,再者,完形填空的能力并不是我们这个模型的目的,我们的目的是计算出合适的嵌入矩阵,这意味着即使这些词语意思不完全相同,但他们的语义关系是比较接近的,比如他们一定都是形容词。
5.2 skip-gram
就是CBOW反过来。
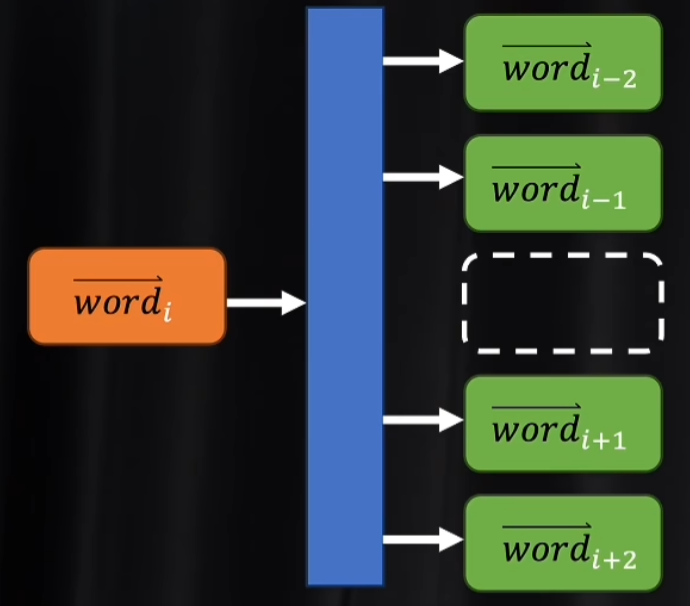
已知一个TOKEN,根据它的词向量,求出上下文对应的TOKEN的分量,看是否和训练数据一致。
这些都是自监督学习,不需要打标签。
6 注意力
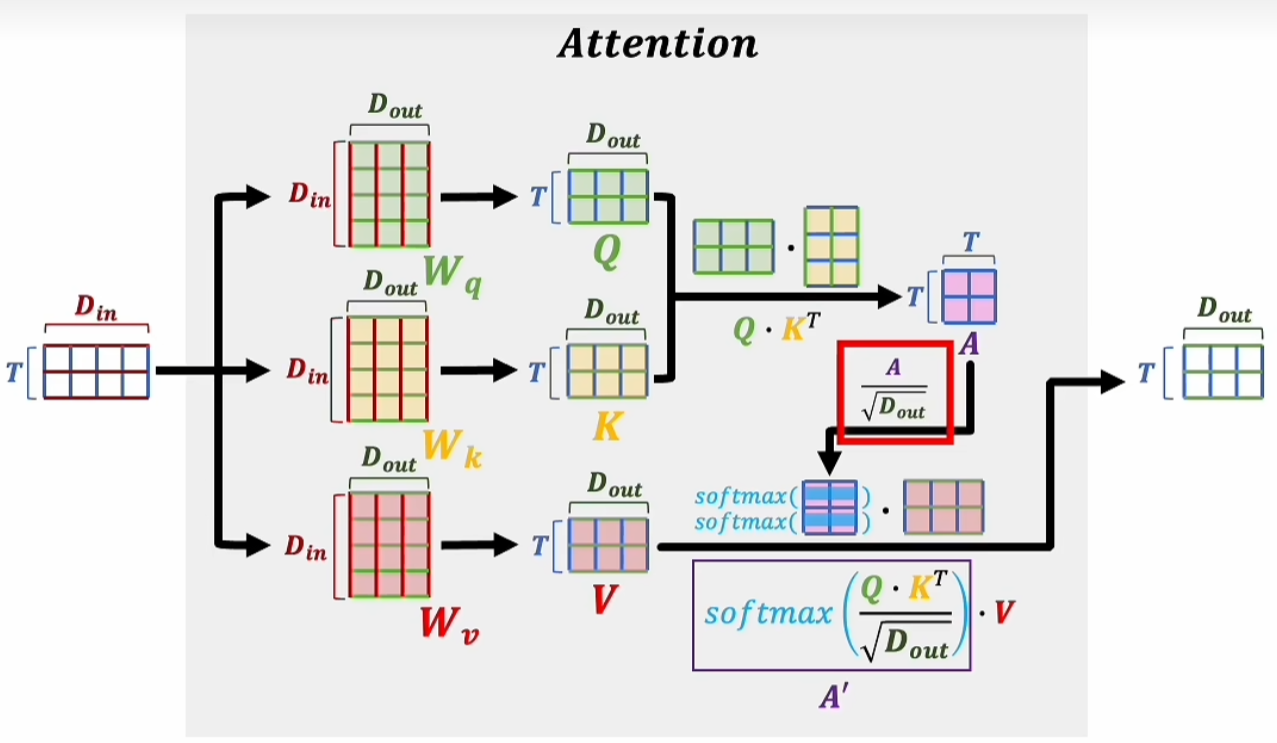
矩阵A也被称作注意力得分,得到A后需要对A中的每一项进行缩放,计算方法:$\frac{A}{\sqrt{D_{out}}}$
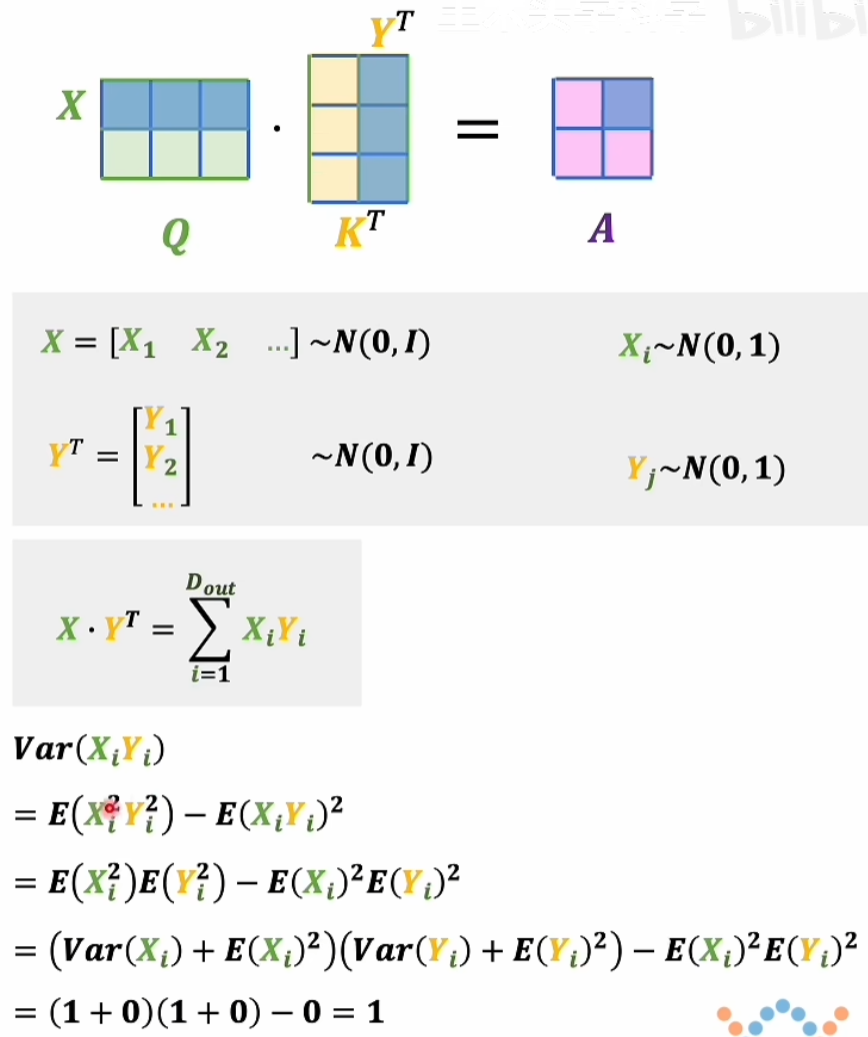
- N(0, 1) 为标准正态分布,期望值是0,标准差是1
- $ Var(x) = E(x^2) - E(x)^2 $
$$ \operatorname{Var}\left(X \cdot Y^T\right)=\sum_{i=1}^{D_{out}} 1=D_{out} $$
$$ X \cdot Y^T \quad \sim N\left(0, D_{out} \cdot I\right) $$
因此 $ XY^T $ 依然是一个多元的高斯分布。
标准差是 $ \sqrt{D_{out} } $ , 因此 $\frac{X_{i}Y_{i}}{\sqrt{D_{out}}} \sim N(0, 1)$
逐行Softmax之后会得到一个按行归一的矩阵,然后再去乘以矩阵V,得到A‘。
$$ A' = \operatorname{softmax}\left(\frac{Q \cdot K^{T}}{\sqrt{D_{out}}}\right) \cdot V $$
6.1 计算的意义
再次明确我们的目标,注意力机制的输入是一组词向量,这一组词向量仅仅具备客观的语义,即字典中的意思,但是它的主观语义取决于这些词向量的组织形式,也就是上下文的作用。
以“美女”这个词举例,其客观语义为“长得很好看”。
美女,加一下微信吧。
美女,麻烦让一让。
在这两个句子中,该词的含义可能略有所不同,而注意力机制需要搞定的,就是识别出那些因为上下文关联,而对词典中原本的客观语义进行调整和改变的幅度。
V表示的是这个TOKEN的客观语义,A’表示的是这段话因为上下文关联而产生的修改系数。
6.2 $ Q \cdot K^{T} $
为什么A‘能表达上下文关联而产生的修改系数呢?
那么回到A的计算。
A其实就是Q和K这两组向量两两之间计算内积,内积就是表示一个向量在另一个向量上的投影,这个投影某种程度上体现的就是两个向量之间的相互关系。
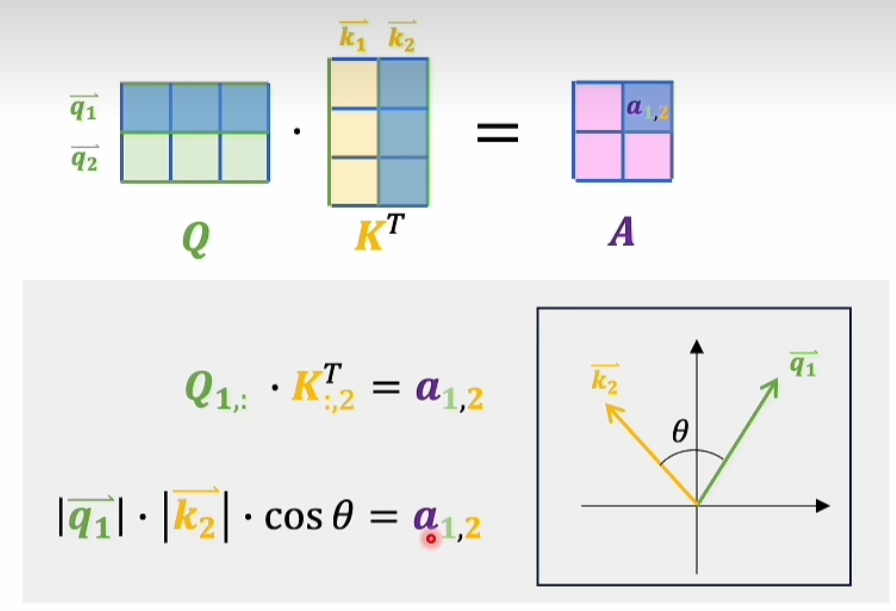
咱们来看这个图
可以看到这个a_12的大小由q和k的模长及两向量夹角决定,因此说它的大小某种程度上就可以决定向量q和k之间的语义关系,如果夹角是零度,两者共线,夹角是九十度,两者正交。
所以说这个矩阵A就是一个关系表,a_12表示的就是第一个词向量和第二个词向量之间的语义关系,以此类推。
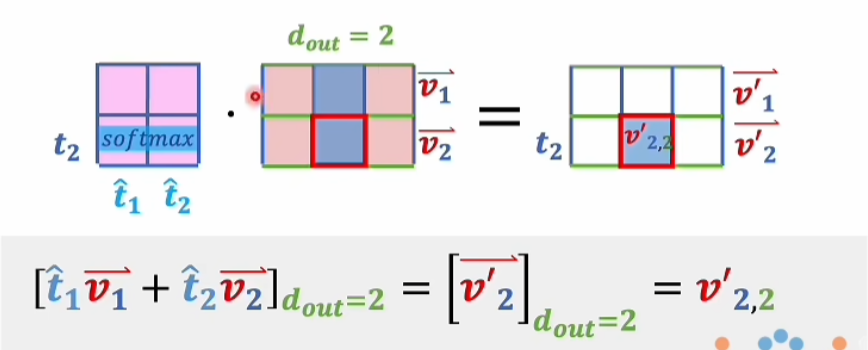
好像,没太看明白。
大致说的是,右边红色框框里的这个 $ v'_{2,2} $ 会受到所有词向量的影响,但是并不是受到所有维度的影响,比如这里只有第二维度。
注意力机制,所以是Q和K得到了这一组词向量自己和自己之间的相互关系,然后再把这个相互关系拿来去修正词向量,让词向量里的每一个维度都能得到修正。语义越接近,代表值越大,也代表了影响越大。这使得这些词向量除了本身在词典中的意思以外,具备了和上下文有关联的主观语义。
7 理解Q和V
不想听了,看看下一个。
8 交叉注意力
自注意力机制根据原有的材料中总结,先理解设定语义,在理解表达语义。
交叉注意力省去了理解设定语义的过程,已有材料提供。
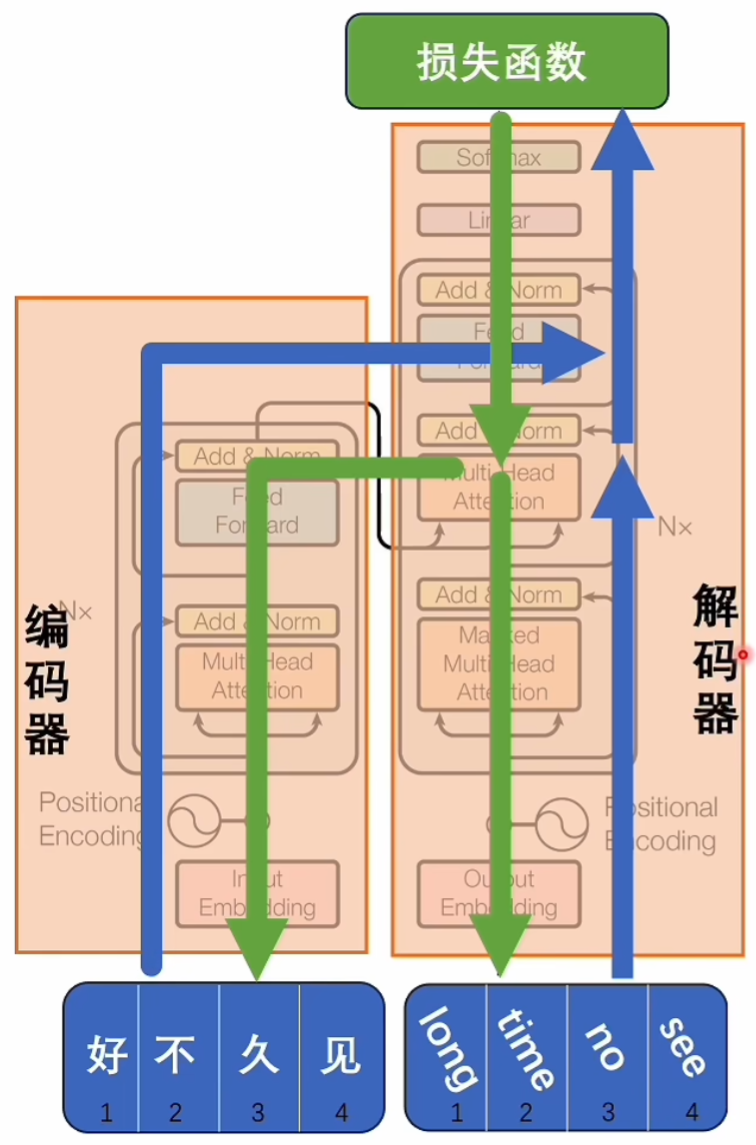
编码器和解码器可以同时训练,损失函数就是这两句话在潜空间中的语义差异,得到损失函数后再进行反向传播,去修改模型里的参数,最终使得这两句话在潜空间中语义相对应。
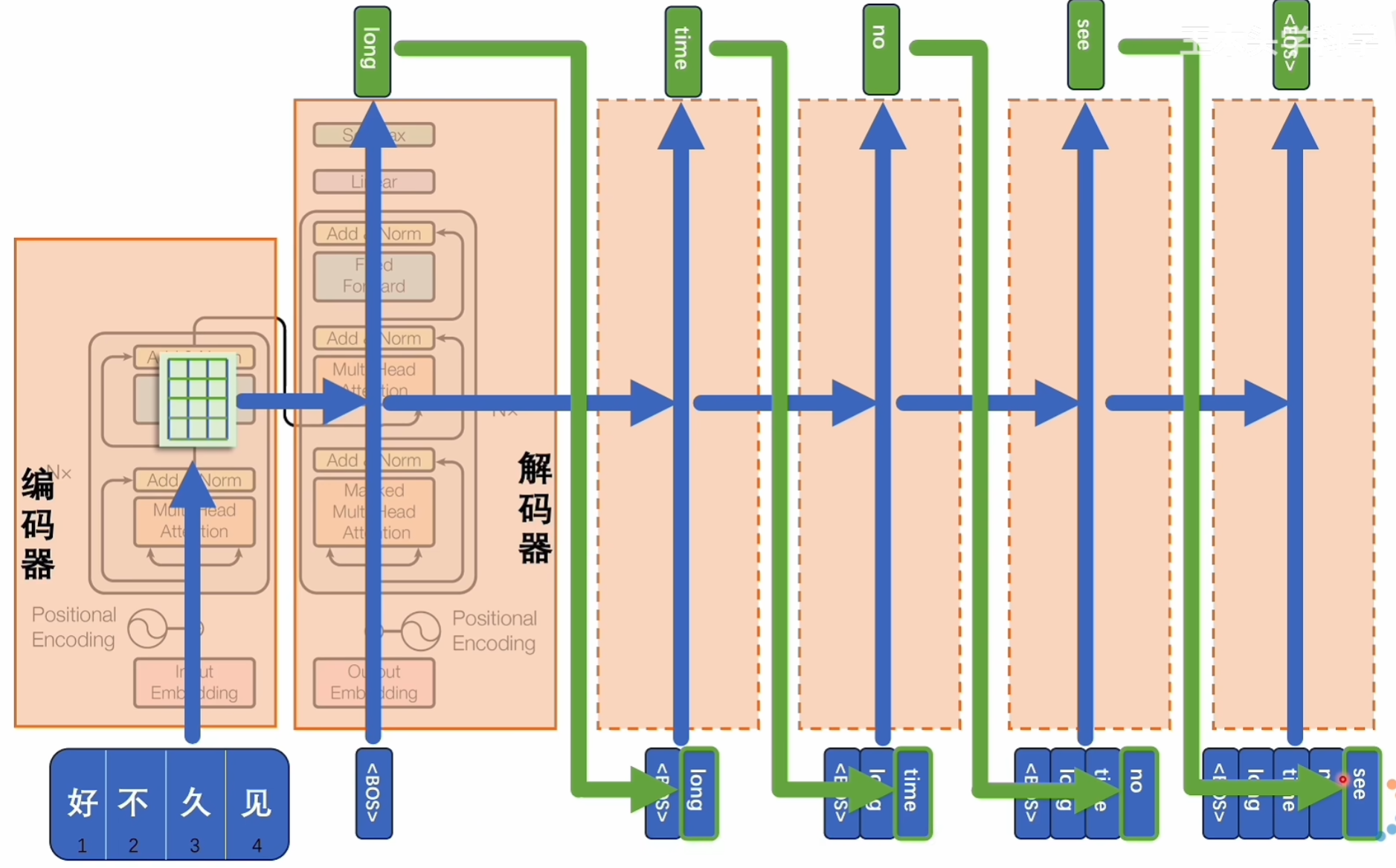
这是推理的过程,由于中英文在进行翻译时,两者的token数量并不总是相等的,这里就使用<BOS>和<EOS>两个符号表示开始和结束,中间可以是任意长度,从而解决这个seq to seq问题。
9 位置编码
位置编码存在的意义:如果没有,Transformer会把所有的token一起放在模型里面并行计算,这样会忽略掉词语的前后顺序所携带的信息。
所以需要保证一组词向量在并行计算的同时,还能体现出他们的先后顺序。
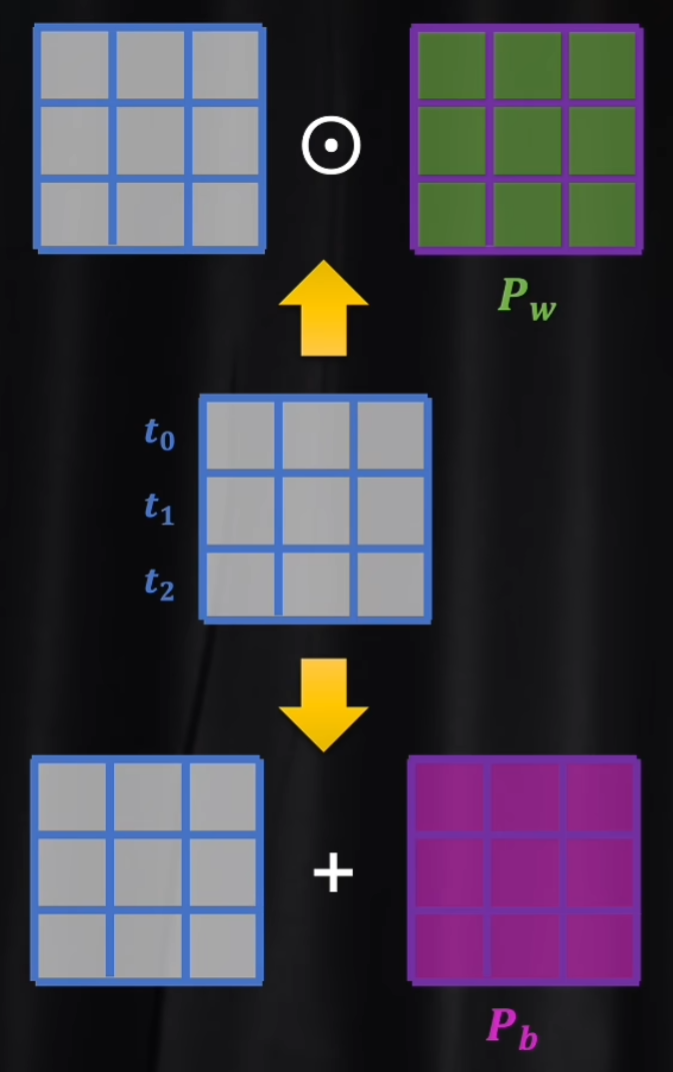
这里提到有两种方法来体现语义的先后顺序。
- 乘法:利用权重增加位置信息
- 加法:利用偏置系数增加位置信息
$\odot$ 是 阿达玛乘积,代表两个矩阵中的元素逐项相乘,所以右边矩阵中每个元素就是左边矩阵对应位置的权重系数。
Transformer采用的是加法,把位置下标,也就是一个一维的自然数集投射到一个与词向量维度相同的连续空间中,依次实现两矩阵的直接相加。
那么怎么把一维自然数集合投射到高维空间?
$$ \boldsymbol{f}(t):= \begin{cases}\sin \left(\frac{1}{10000^{2 \cdot i / D}} \cdot t\right), & \text { 如果 } d=\mathbf{2} i \\ \cos \left(\frac{1}{10000^{2 \cdot i / D}} \cdot t\right), & \text { 如果 } d=\mathbf{2} i+\mathbf{1}\end{cases} $$
这是论文中的公式。
还没写完。